20. 10억 개 전화번호에서 이름 찾기 : 이진 검색
이진검색 :
알고리즘인데 정렬되어 있는 리스트에서 탐색 범위를 절반씩 좁혀가며 데이터를 탐색(검색)하는 방법.
단점 : 배열 내부의 데이터가 정렬되어 있어야 사용 가능한 알고리즘.
But, 검색이 반복될 때마다 목표값을 찾을 확률이 두배가 되므로 속도 빠름.
이진검색 성능 :
한번 비교가 이루어질 때마다, 범위는 1/2로 감소. 데이터의 집합 크기를 n으로 두고, 반복 횟수를 k로 가정시 수식은 아래와 같다.


데이터 집합의 크기 n을 2로 몇 번을 나누어야 1이 되는가의 식이다.
데이터 집합의 크기가 1024라면 10번의 탐색으로 데이터를 찾아낼 수 있다. (2의 10제곱 = 1024)
선형탐색 : 이진탐색

선형 탐색 : 리스트의 처음부터 끝까지 순서대로 하나씩 탐색을 진행함.
이진 탐색 : 정렬된 리스트에서 중간값과 비교해 반씩 제외하며 탐색을 하는 알고리즘.
=> 배열의 길이가 증가할수록 선형과 이진탐색 속도 격차는 벌어진다.

검색을 쉽게 만드는 정렬 :
선택 : 퀵
-선택 정렬-
- 주어진 항목들이 정렬되어 있지 않으면 이진 검색을 할 수 없음.
- 정렬(sorting)은 항목을 순서대로 배열해서 검색이 빨리 실행될 수 있도록 함.
- 선택 정렬(Selection Sort)은 아직 정렬되지 않은 항목 중에서 다음 항목을 계속 선택함.
- 알고리즘을 연구하는 컴퓨터과학자들은 비관론자라서 지름길 없이 모든 작업을 수행해야 하는 최악의 경우를 가정함.
- [항목을 훑어보는 횟수] = [N + N-1 + N-2 + ... + 1] = [N * (N+1) / 2].
- 일의 양은 N^2 , 계수를 제외해서 최고차항인 2차(quadratic)인 증가율.
=> 배열의 모든 요소를 앞부터 차례대로 정렬된 배열 부분과 비교해 자신의 위치를 찾아 삽입.
주어진 리스트 중에 최소값을 찾고 그 값을 맨 앞에 위치한 값과 교체하는 방식으로 진행하는 정렬방법이며,
다른 정렬들과 다르게 비효율적.(최선의 경우조차 모두 비교하기 때문임.)

-퀵-
기준(pivot)을 설정해 크고 작은 숫자를 교환하고 리스트를 분할.


1. 리스트 안에 있는 한 요소를 선택하고 고른 원소를 피벗(pivot).
2. 피벗 기준으로 피벗보다 작은 요소들은 모두 피벗의 왼쪽으로 옮기고 피벗보다 큰 요소들은 오른쪽으로 옮긴다.
- left는 오른쪽으로, right는 왼쪽으로 이동
- left는 피벗보다 큰 수를 만나거나 피벗을 만나면 멈춤.
- right는 피벗보다 작은 수를 만나거나 피벗을 만나면 멈춤.

- left와 right가 멈췄을 대, left가 right보다 왼쪽에 있다면 left와 right 값을 교환함.
- 이후 left를 오른쪽으로 한 칸, right를 왼족으로 한 칸 이동하고 이 과정을 left가 right보다 오른쪽으로 올 때까지 반복한다.
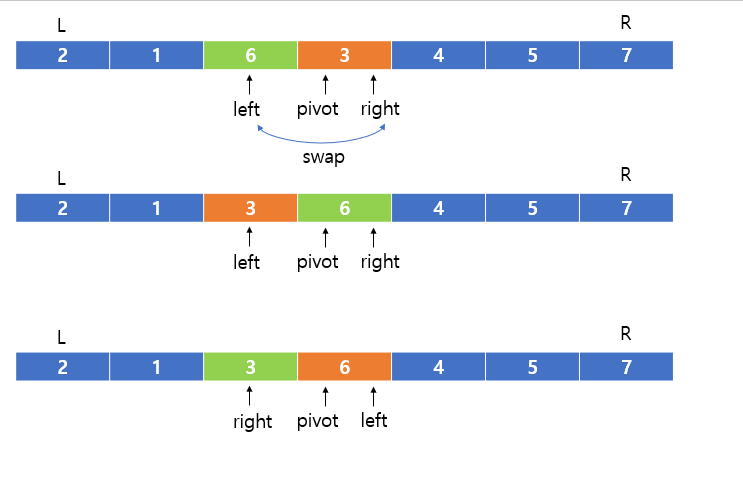
- 6 > 3 이므로 6에서 left가 멈춤
- right는 피벗을 만나 멈춤
- left가 right보다 왼쪽에 있으므로 left와 right 값을 교환함.
- left를 오른쪽으로 한 칸, right를 왼쪽으로 한 칸 이동함.
- left가 right보다 오른쪽에 있으므로 종료함.
3. 피벗을 제외한 왼쪽, 오른쪽 리스트를 재정렬함.
- 분할된 왼쪽 리스트와 오른쪽 리스트도 다시 피벗을 정하고 피벗을 기준으로 2개의 부분리스트로 나눔.
- 재귀를 사용하여 부분 리스트들이 더 분할이 불가능 할 때까지 반복함.

- right > L 이면 L부터 right까지 위 사진 과정을 재귀적 반복함.
- left < L 이면 left부터 R까까지 위 사진 과정을 재귀적 반복함.

- 좌측 배열 정렬 과정
- left는 2에서 멈춤
- right는 피벗에서 멈춤
- left가 right보다 좌측에 있어 둘 교환함.
- left를 우측으로 한 칸, right를 좌측으로 한 칸 이동함.
- left가 right보다 우측에 있으며로 종료함.
- right <L 이므로 좌측배열(L부터 right)은 다시 재귀적으로 정렬할 필요 X
- left < L 이므로 left부터 R까지 다시 재귀적으로 정렬.
- 우측 배열 정렬 과정
- left는 6에서 멈춤
- right 피벗에서 멈춤
- left가 right보다 왼쪽에 있어 둘을 교환함.
- left를 우측으로 한 칸, right를 좌측으로 한 칸 이동.
- left가 right보다 우측에 있어 종료함.
- right < L 므로 좌측배열(L부터 right)은 다시 재귀적 정렬 필요X
- right < L이므로 left부터 R까지 다시 재귀적 정렬.

=> 오름차순으로 정렬된다.
